그림으로 설명하는 펑터, 아플리커티브, 모나드
[ 원글 : http://adit.io/posts/2013-04-17-functors,_applicatives,_and_monads_in_pictures.html ]
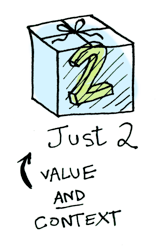
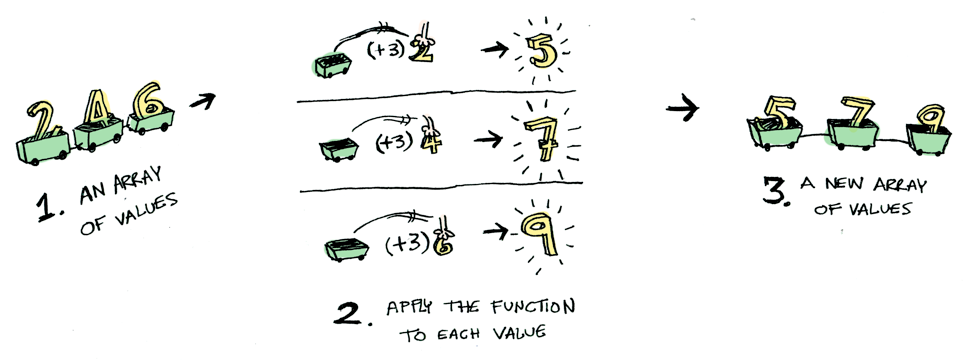
여기 간단한 값(value)의 예가 있다: 
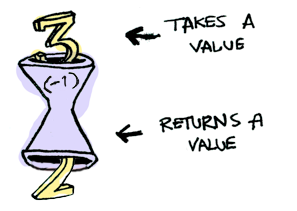
이 값에 함수를 적용해 보자: 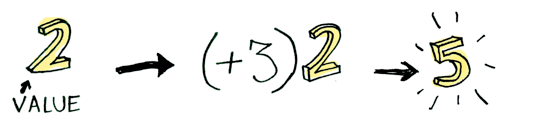
간단하지요. 어떤 문맥 안에 값을 놓고 반복해보자. 당분간 문맥을 값을 집어 넣을 수 있는 박스로 생각하자.:
함수를 이 값에 적용하면 그 문맥에 따라 다른 결과를 얻을 것이다. 펑터, 어플리커티브, 모나드, 애로우 등 모든 개념이 이 아이디어를 기초로 하고 있다. Maybe 데이터 타입은 두 가지 연관된 문맥을 정의한다:
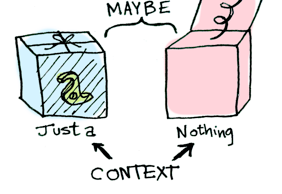
data Maybe a = Nothing | Just a
Just a와 Nothing일 때 함수를 적용하는 방법이 다르다는 것을 바로 알 수 있을 것다. 먼저 펑터에 대해 얘기하자!
펑터(Functors)
문맥 안에 값을 감싸두면 보통 함수를 그 값에 적용할 수 없다:

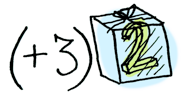
이런 상황에서 fmap이 필요하다. fmap은 문맥을 알고 있다. fmap을 통해 문맥 속의 값에 함수를 적용할 수 있다. 함수 (+3)을 Just 2에 적용한다고 가정해보자. fmap을 사용하자:
> fmap (+3) (Just 2)
Just 5
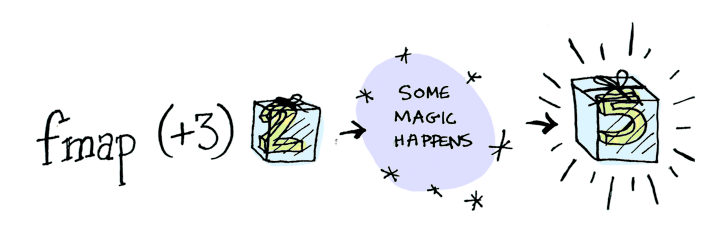
두둥! fmap은 어떻게 하는지 가르쳐준다. 그런데 fmap은 이 함수를 적용하는 법을 어떻게 알 까?
펑터가 뭐지, 진짜?
펑터는 타입클래스다. 여기 그 정의가 있다:
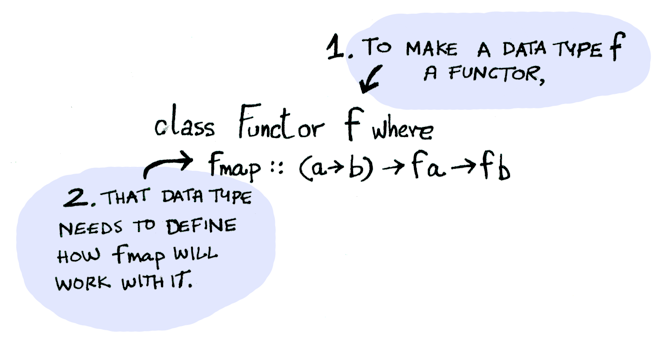
Functor는 fmap을 적용하는 방법을 정의하는 데이터타입이다. 다음은 fmap의 동작 방식이다:
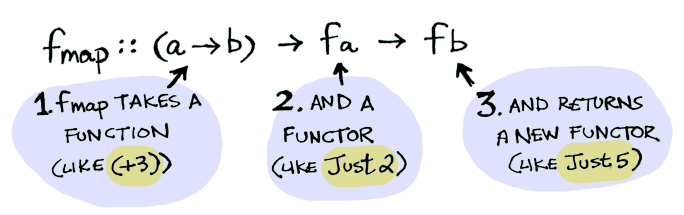
따라서 이렇게 할 수 있다:
> fmap (+3) (Just 2)
Just 5 Maybe는 펑터이기 때문에 마법같이 fmap으로 이 함수를 적용한다. 이 펑터로 fmap을 Just들과 Nothing들에 어떻게 함수를 적용하는지 정한다:
instance Functor Maybe where
fmap func (Just val) = Just (func val)
fmap func Nothing = Nothing
fmap (+3) (Just 2)라고 코드의 동작을 다음과 같이 설명할 수 있다:
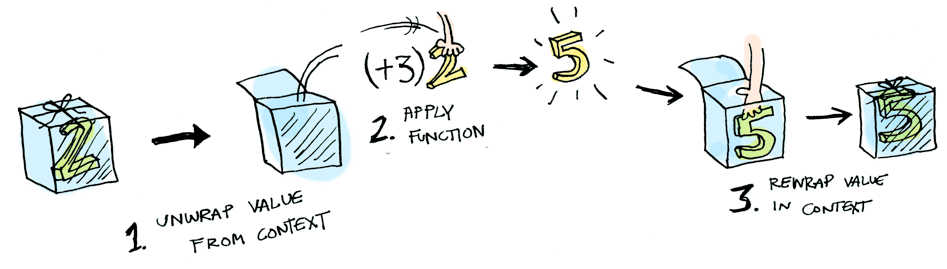
fmap으로 (+3)을 Nothing에 적용해볼까?
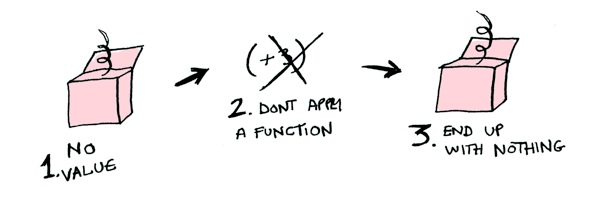
> fmap (+3) Nothing
Nothing

빌 오라일리, Maybe 펑터에 대해 전혀 알고 있지 않은
영화 매트릭스의 모피어스처럼 fmap은 무엇을 해야할지 알고 있다. Nothing을 가지고 시작하면 Nothing으로 끝날 뿐이다! fmap은 젠(zen)이다. 이제 Maybe 데이터타입이 존재하는 이유가 있다. 예를 들어, Maybe가 없는 언어로 데이터베이스 레코드를 다룬다고 하자:
post = Post.find_by_id(1)
if post
return post.title
else
return nil
end
하스켈로 옮겨보면:
fmap (getPostTitle) (findPost 1)
만일 findPost에서 포스트를 반환하면 getPostTitle로 그 제목을 얻을 수 있다. 만일 findPost에서 아무것도 반환하지 않으면 (Nothing을 반환하면) Nothing을 반환할 것이다. 꽤 깔끔하죠? <$>은 fmap의 인픽스(infix) 버전으로, 위 코드 대신 다음과 같이 작성할 수 있다:
getPostTitle <$> (findPost 1)
다른 예를 보자: 함수를 리스트에 적용하면 어떻게 되나?
리스트도 펑터다! 여기 그 정의가 있다:
instance Functor [] where
fmap = map
오케이, 마지막 예: 함수에 다른 함수를 적용하면 어떨까?
fmap (+3) (+1)
여기 함수가 있다:
여기 다른 함수에 적용할 함수가 있다:
그 결과는 단지 또다른 함수다!
> import Control.Applicative
> let foo = fmap (+3) (+2)
> foo 10
15
따라서 함수도 펑터다!
instance Functor ((->) r) where
fmap f g = f . g
fmap을 함수에 사용하면 그 결과는 함수 조합이 된다!
어플리커티브(Applicatives)
어플리커티브는 그 다음 레벨로 데려다준다. 어플리커티브를 사용하면, 펑터처럼, 값을 어떤 문맥 안에 감쌀 수 있다:

그러나 함수도 문맥 안에 감쌀 수 있다!

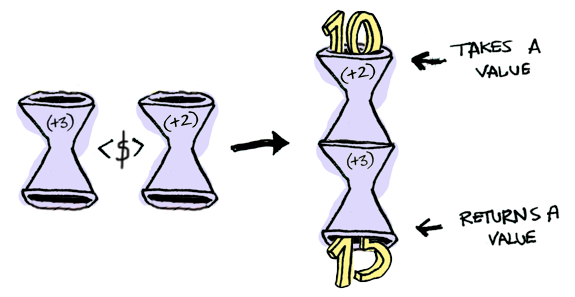
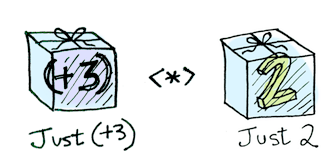
자, 이해해보자. Control.Applicative에서 <*>를 두어 어떤 문맥에 감싸져 있는 함수를 관련된 문맥 속에 있는 값에 적용하는 방법을 지정한다:
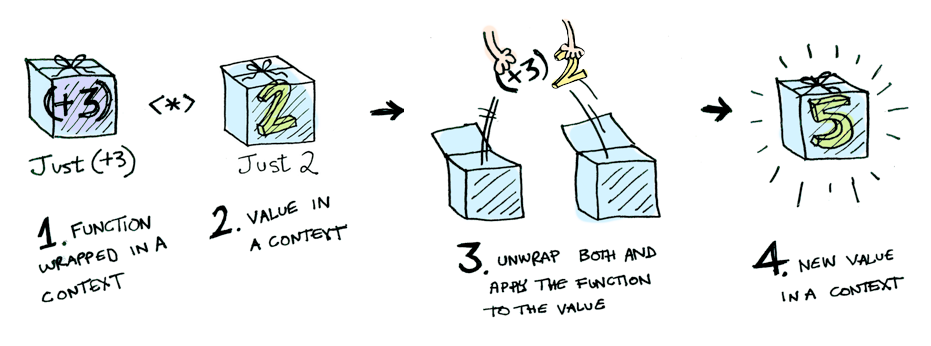
예컨데:
Just (+3) <*> Just 2 == Just 5
<*>를 사용하면 재미있는 상황이 벌어질 수 있다. 예를 들어:
> [(*2), (+3)] <*> [1, 2, 3]
[2, 4, 6, 4, 5, 6]
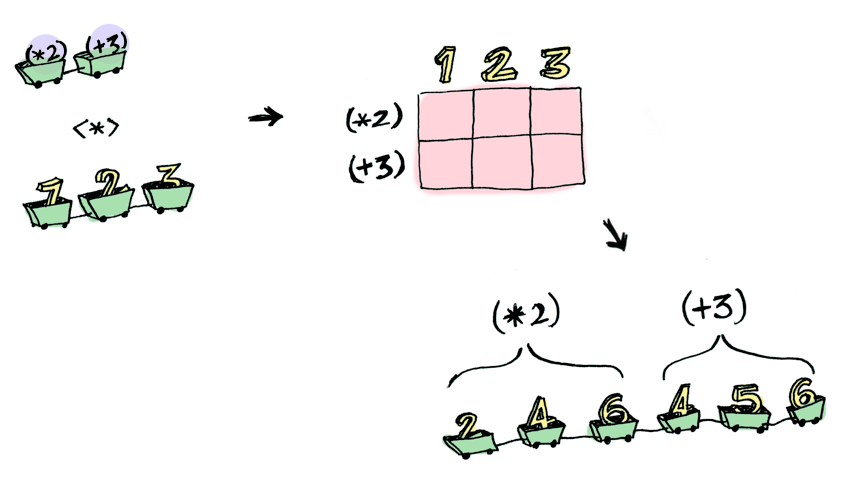
펑터로는 할 수 없지만 어플리커티브로 할 수 있는 것이 있다. 두 개의 인자를 받는 함수를 문맥에 감싸져 있는 두 개의 값에 어떻게 적용할 수 있을까?
> (+) <$> (Just 5)
Just (+5)
> Just (+5) <$> (Just 4)
ERROR ??? WHAT DOES THIS EVEN MEAN WHY IS THE FUNCTION WRAPPED IN A JUST
어플리커티브:
> (+) <$> (Just 5)
Just (+5)
> Just (+5) <*> (Just 3)
Just 8 Applicative는 Functor보다 유연하다. "다 큰 남자는 인자를 몇 개 받든 상관없이 어떠한 함수라도 사용할 수 있어야 한다."라고 마치 말하는 것 같다. "<$>와 <*>를 가지고 임의 개수의 값을 받는 어떤 함수에 포장된 값들을 전달하고 그 결과로 포장된 값을 반환 받을 수 있다!"
> (*) <$> Just 5 <*> Just 3
Just 15
이러한 똑같은 일을 하는 liftA2라 부르는 함수가 있다:
> liftA2 (*) (Just 5) (Just 3)
Just 15
모나드(Monads)
모나드를 배우는 방법:
- 컴퓨터 과학 분야의 박사학위를 얻은 다음,
- 그것을 던져 버린다. 왜냐하면 여기 설명에서는 그 학위가 필요하지 않기 때문에!
모나드는 새로운 방법을 추가한다.
펑터는 함수를 포장된 값에 적용한다:
어플리커티브는 포장된 함수를 포장된 값에 적용한다:
모나드는 포장된 값을 반환하는 함수에 포장된 값을 적용한다.모나드는 바인드라고 읽는 함수로 이것을 한다.
예를 살펴보자. Maybe는 모나드다:

half는 짝수에 대해 동작하는 함수라 가정하자:
half x = if even x
then Just (x `div` 2)
else Nothing
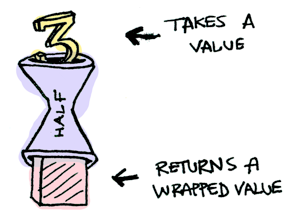
포장된 값을 전달하면 무슨 일이 벌어질까?

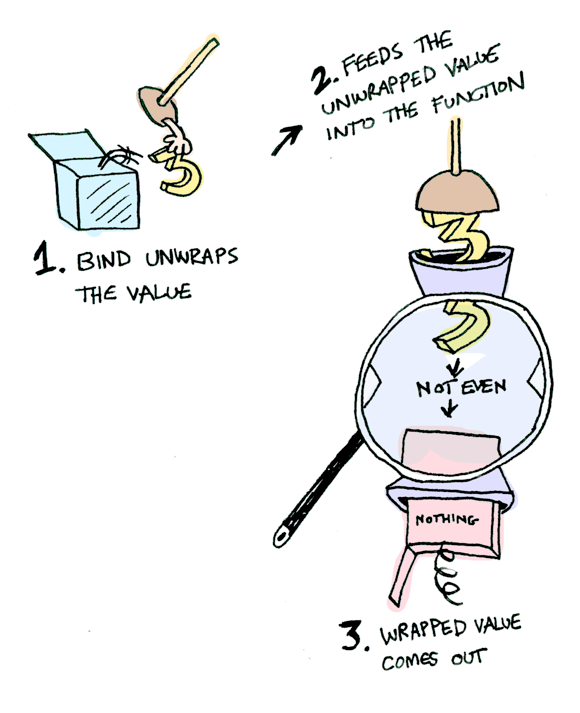
함수 >>=를 사용해서 포장된 값을 함수로 밀어낼 수 있다. 함수 >>=의 사진이 여기 있다:

동작 방식을 설명한다:
> Just 3 >>= half
Nothing
> Just 4 >>= half
Just 2
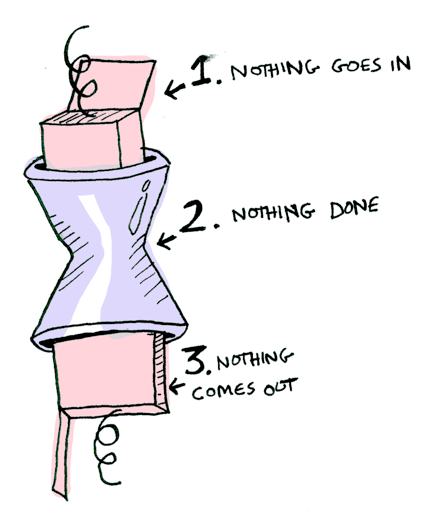
> Nothing >>= half
Nothing
내부에서 어떤 일이 벌어지고 있나? Monad는 타입클래스다. 부분적으로 아래와 같이 정의한다:
class Monad m where
(>>=) :: m a -> (a -> m b) -> m b
바인드 함수 >>=는:

따라서 Maybe는 Monad다:
instance Monad Maybe where
Nothing >>= func = Nothing
Just val >>= func = func val
아래에서 Just 3에 대한 동작을 설명한다!
Nothing을 주는 경우는 더 간단하다:
이런 함수 호출들을 차례로 묶을 수 있다:
> Just 20 >>= half >>= half >>= half
Nothing


쿨! 이제 Maybe는 펑터, 어플리커티브, 모나드라는 것을 알았다.
이제 다른 예를 반복해서 살펴보자: IO 모나드:
특히 3가지 함수들. getLine은 특별한 인자 없이 사용자 입력을 받는다:

getLine :: IO String
readFile은 파일 이름 문자열을 인자로 받고 그 파일 내용을 반환한다:

readFile :: FilePath -> IO String
putStrLn은 문자열을 받아 출력한다:

putStrLn :: String -> IO ()
세가지 모든 함수들은 일반 값을 받아(또는 받지 않고) 포장된 값을 반환한다. 이 함수들을 바인드 함수 >>=를 사용하여 차례대로 묶을 수 있다!
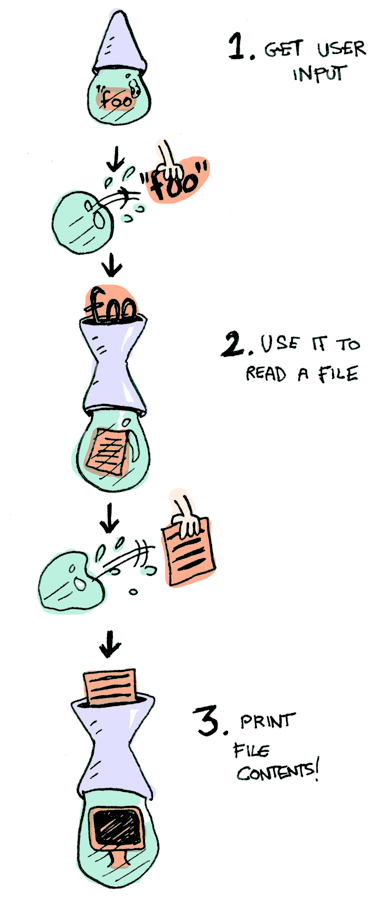
getLine >>= readFile >>= putStrLn
하스켈 언어는 모나드를 사용하는데 편리한 구문, do 표기법을 제공한다:
foo = do
filename <- getLine
contents <- readFile filename
putStrLn contents
결론
- 펑터는 Functor 타입클래스를 구현하는 데이터 타입이다.
- 어플리커티브는 Applicative 타입클래스를 구현하는 데이터 타입이다.
- 모나드는 Monad 타입클래스를 구현하는 데이터 타입이다.
- Maybe는 이 세가지를 모두 구현한다. 따라서 펑터이고, 어플리커티브이며, 모나드이다.
이 세가지의 차이점은 무엇인가?

- 펑터: fmap이나 <$>를 사용하여 함수를 포장된 값에 적용한다.
- 어플리커티브: <*>나 liftA를 사용하여 포장된 함수를 포장된 값에 적용한다.
- 모나드: >>=나 liftM을 사용하여 포장된 값을 리턴하는 함수를 포장된 값에 적용한다.
자, 여기까지 설명을 들었다면 모나드가 쉽고 SMART IDEA(tm)라는 점에 우리 모두 동의할 것이라 생각한다. 이 가이드로 여러분의 궁금증을 일부 해소했다면 이제 더 심화된 내용을 살펴볼 차례다. LYAH의 모나드 섹션을 살펴보라. 이 가이드에서 넘어갔던 많은 것이 있다. Miran은 자세한 설명을 해줄 것이다.
'Haskell' 카테고리의 다른 글
| 하스켈 프로그래밍 스터디 계획 (0) | 2015.08.31 |
|---|---|
| 하스켈 프로그래밍(Haskell) 커뮤니티 (0) | 2015.08.31 |

